Library sort

Library sort
Class	Sorting algorithm
Data structure	Array
Worst case performance	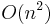$O(n^2)$
Best case performance	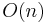$O(n)$
Average case performance	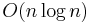$O(n\log n)$
Worst case space complexity	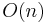$O(n)$

Library sort, or gapped insertion sort is a sorting algorithm that uses an insertion sort, but with gaps in the array to accelerate subsequent insertions. The name comes from an analogy:^[1]

Suppose a librarian were to store his books alphabetically on a long shelf, starting with the As at the left end, and continuing to the right along the shelf with no spaces between the books until the end of the Zs. If the librarian acquired a new book that belongs to the B section, once he finds the correct space in the B section, he will have to move every book over, from the middle of the Bs all the way down to the Zs in order to make room for the new book. This is an insertion sort. However, if he were to leave a space after every letter, as long as there was still space after B, he would only have to move a few books to make room for the new one. This is the basic principle of the Library Sort.

The algorithm was proposed by Michael A. Bender, Martín Farach-Colton, and Miguel Mosteiro in 2006.^[2]

Like the insertion sort it is based on, library sort is a stable comparison sort and can be run as an online algorithm; however, it was shown to have a high probability of running in O(n log n) time (comparable to quicksort), rather than an insertion sort's O(n²). Its implementation is very similar to a skip list. The drawback to using the library sort is that it requires extra space for the gaps.

References

^ Budd, Timothy A., An Active Learning approach to Data Structures using C, http://classes.engr.oregonstate.edu/eecs/winter2009/cs261/Textbook/Chapter14.pdf
^ Bender, M. A., Farach-Colton, M., and Mosteiro M. (2006). "Insertion Sort is O(n log n)". Theory of Computing Systems 39 (3): 391. doi:10.1007/s00224-005-1237-z.

External links

Gapped Insertion Sort

Sorting algorithms

Theory	Computational complexity theory Big O notation Total order Lists Stability Comparison sort Adaptive sort Sorting network Integer sorting

Exchange sorts	Bubble sort Cocktail sort Odd–even sort Comb sort Gnome sort Quicksort Stooge sort Bogosort

Selection sorts	Selection sort Heapsort Smoothsort Cartesian tree sort Tournament sort Cycle sort

Insertion sorts	Insertion sort Shellsort Tree sort Library sort Patience sorting

Merge sorts	Merge sort Polyphase merge sort Strand sort

Distribution sorts	American flag sort Bead sort Bucket sort Burstsort Counting sort Pigeonhole sort Proxmap sort Radix sort Flashsort

Concurrent sorts	Bitonic sorter Batcher odd–even mergesort Pairwise sorting network

Hybrid sorts	Timsort Introsort Spreadsort UnShuffle sort JSort

Quantum sorts	Spaghetti sort

Other	Bogosort Topological sorting Pancake sorting